Introduction
Quand on n’utilise pas le même mot de passe sur tous les sites/programmes, il n’est pas facile de tous les connaître par cœur. Fort heureusement, il existe presque toujours une procédure de récupération relativement facile lorsque l’on a un trou de mémoire, ce qui n’est malheureusement pas le cas des fichiers numériques et notamment les archives comme nous en avons récemment fait l’expérience.
Rappelons qu’il y a de nombreux moyens de protéger ses données : TrueCrypt est par exemple un excellent logiciel libre pour chiffrer des informations, d’autant plus qu’il supporte maintenant les instructions AES-NI. Pourtant, le chiffrement des archives est encore la solution la plus répandue.
Le niveau de sécurité est parfois mal compris : pour peu que l’on soit paranoïaque en matière de protection, on choisit le chiffrement le plus complexe en pensant que c’est aussi le plus sûr. L’AES-256 devrait donc être supérieur à l’AES-128 et pourtant, le problème est plus subtil. On peut représenter le chiffrement comme un gros coffre-fort : son épaisseur est gage de sécurité … tout comme la clé qui permet de l’ouvrir. La longueur et la complexité du mot de passe sont donc deux critères à ne surtout pas négliger.
Une majorité de gens estiment qu’un mot de passe contenant huit caractères suffit à tenir les hackers à distance, ce qui n’est pas tout à fait vrai comme nous allons le voir.
Configuration du test
| Composants | |
|---|---|
| Processeur | Intel Core i5-2500K (Sandy Bridge), 3,3 GHz, LGA 1155, 6 Mo de cache L3 partagés |
| Carte mère | Asus P8P67 Deluxe |
| DRAM | Kingston Hyper-X 8 Go (2 x 4 Go) DDR3-1333, 1,5 Volt |
| Stockage | Samsung 470 256 GB |
| Cartes graphiques | Palit GeForce GTX 460 1 Go Asus GeForce GTX 570 1,28 Go AMD Radeon HD 5870 1 Go |
| Alimentation | Seasonic 760 Watts, 80 PLUS |
| Logiciels et pilotes | |
| Os | Windows 7 Ultimate 64 bits |
| DirectX | Version 11 |
| Graphiques | ForceWare 270.51 Catalyst 11.4 |
| Archivage & récupération | |
|---|---|
| Visual Zip Password Recovery Processor | Version 6.2 |
| Advanced Archive Password Recovery | Version 4.53 |
| Accent Zip Password Recovery | Version 2.01 |
| Accent RAR Password Recovery | Version 2.01 |
| Parallel Password Recovery | Version 1.6.0 |
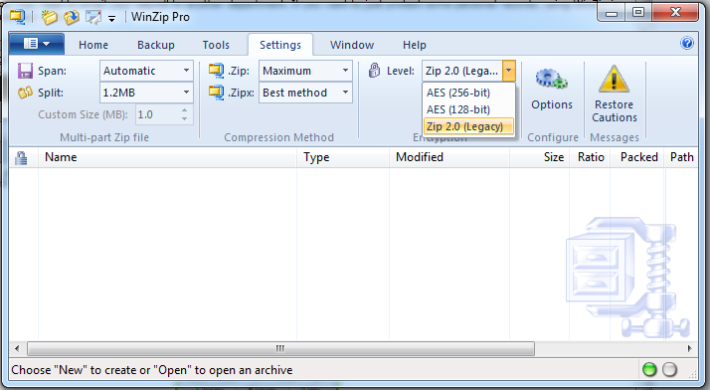
| WinZip | Version 15.5 Pro Chiffrement: Zip 2.0, AES-128, AES-256 Compression: aucune, Zipx/PPMd, Zip/deflate |
| WinRAR | Version 4.00 64 bits Chiffrement: AES-128 Compression: Normal, Stocker |
Soulignons que WinZip propose trois types de chiffrement : Zip 2.0, AES-128 et AES-256 ainsi que plusieurs niveaux de compression. WinRAR est bien plus simple dans la mesure où il se contente uniquement de l’AES-128 (ainsi que les réglages de compression). On verra comment ces paramètres influent sur la récupération d’un mot de passe.
Cryptage : WinZip et WinRAR
Les archives chiffrées type WinZip/WinRAR sont généralement moins sûres qu’un disque dur intégralement chiffré, parce qu’il s’agit de deux approches différentes.
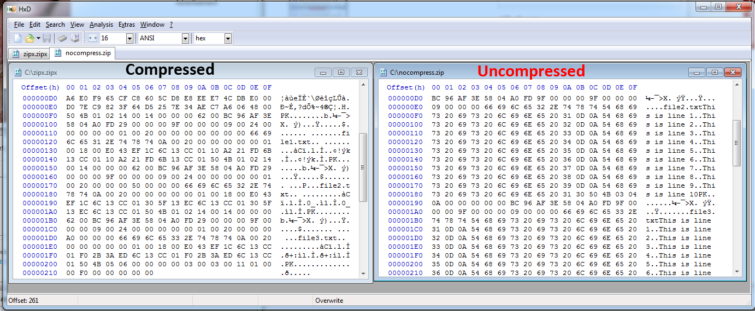
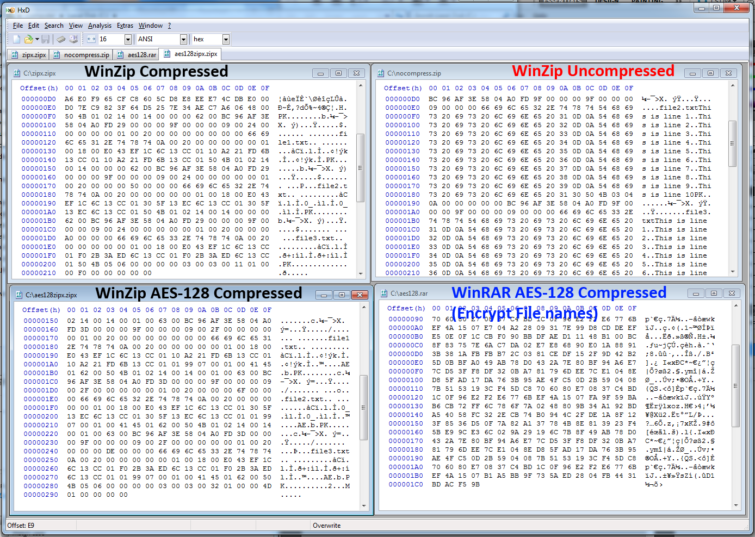
La compression des données consiste à coder un ou plusieurs fichiers tout en supprimant les redondances de manière à optimiser l’espace de stockage. On peut voir la différence en comparant les fichiers dans un éditeur hexadécimal :
Le chiffrement n’est pas effectué au niveau du contenant pour WinZip, d’où le fait que le contenu de l’archive soit visible puisque le nom des fichiers n’est pas protégé.
WinRAR s’appuie sur le même concept, mais propose le chiffrement des noms de fichiers. L’accès au contenant est alors sécurisé par un mot de passe.
Le nom des fichiers fait partie de ce qu’on appelle les métadonnées. Une des différences entre WinRAR et WinZip tient au fait que les métadonnées apparaissent en texte brut avec ce dernier.
Ceci ne rend pas nécessairement WinRAR plus sûr pour autant, mais un hacker persistant essaiera spontanément d’utiliser les métadonnées vu qu’elles ne sont généralement pas chiffrées et permettent de trouver des informations précieuses. Restera ensuite à concevoir un exploit à partir des failles identifiées dans la méthode de chiffrement.
Ce constat est peu rassurant, mais il ne faut pas s’inquiéter à partir du moment où l’on allie un mot de passe complexe à une méthode de chiffrement sûre (AES-128 ou AES-256). En parallèle, mieux vaut éviter des noms évocateurs comme « relevés de compte 2011 » lorsque l’on cherche à ne pas attirer l’attention. Mais à trop vouloir en faire, que se passe-t-il lorsque l’on a oublié comment accéder aux données que l’on a protégé soi-même ?
Résistance des mots de passe
On peut concevoir le chiffrement de données comme une grille de sudoku : plus la complexité est grande, plus il sera difficile d’en venir à bout. Deux approches permettent de s’y attaquer.
En premier lieu, les hackers essaient de trouver une sorte de motif dans le chiffrement. Cette approche se subdivise en plusieurs types comprenant notamment les attaques par canaux auxiliaires dont on entend parfois parler. Ces méthodes sont complexes au point d’être inaccessibles à l’utilisateur moyen.
L’autre approche est bien plus primitive puisqu’il s’agit d’un processus répétitif d’essai/erreur : on parle alors d’attaque par force brute. Pour reprendre l’exemple du sudoku, cela revient à générer toutes les combinaisons de chiffres possibles pour résoudre la grille. Il existe des moyens de freiner ce type d’attaque en masquant les identifications réussies, mais il s’agit d’un luxe que ne peuvent pas se permettre des programmes grand public comme WinZip et WinRAR. Vu que le nombre d’erreurs n’est pas limité, la question n’est pas de savoir si le mot de passe pourra être retrouvé mais dans quel délai.
| Caractères disponibles (hors lettres accentuées) | Combinaisons à deux caractères | Combinaisons à quatre caractères | Combinaisons à six caractères |
|---|---|---|---|
| Minuscules | 676 | 456 976 | 308 915 776 |
| Minuscules et majuscules | 2704 | 7 311 616 | 19 770 609 664 |
| Minuscules, majuscules et nombres | 3844 | 14 776 336 | 56 800 235 584 |
| Carcatères ASCII | 8836 | 78 074 896 | 689 869 781 056 |
Les attaques par force brute s’appuient sur les probabilités ; vu que le nombre de combinaisons augmente en fonction de la longueur du mot de passe, la notion de permutation est primordiale. Admettons par exemple les mots de passe comme des anagrammes : avec les lettres a, b et c, on trouve six combinaisons ([a,b,c], [a,c,b], [b,a,c], [b,c,a], [c,a,b] et [c,b,a]).
Le calcul du nombre de possibilités est simple : n(taille du mot de passe), sachant que « n » correspond au nombre de caractères. Comme on peut le voir dans le tableau ci-dessus, les 26 lettres de l’alphabet en minuscules et majuscules suffisent à atteindre plusieurs milliards de combinaisons. Si l’on étend la sélection aux caractères spéciaux et chiffres (les 128 caractères ASCII), on arrive alors à plusieurs centaines de milliards. N’oublions pas non plus qu’à défaut de connaitre la taille du mot de passe, il faudra tester toutes les combinaisons allant de un à x caractères.
Cracker un mot de passe avec le CPU
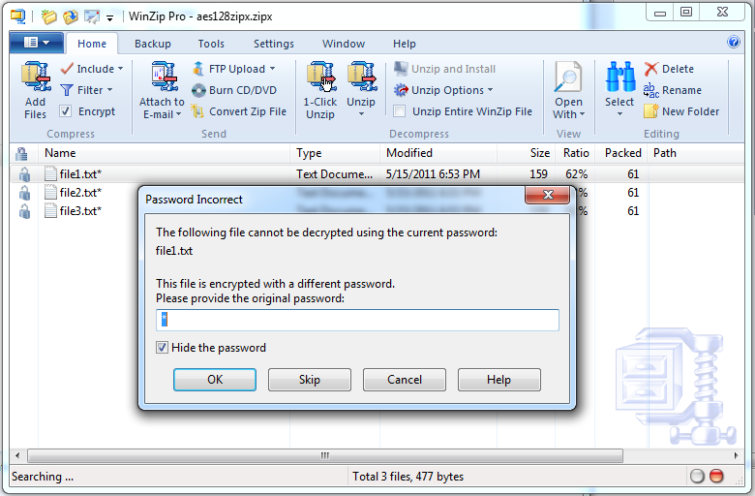
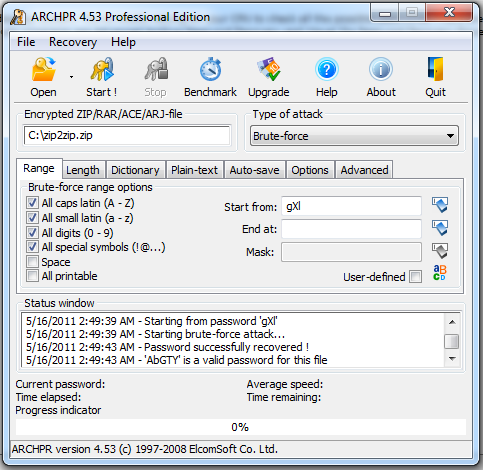
Il existe une myriade de programmes pour récupérer un mot de passe, parmi lesquels Advanced Archive Password Recovery et Visual Zip Password Recovery Processor. Nous avons utilisé le premier pour récupérer un mot de passe à 7 caractères sur une archive WinZip en 20 minutes. Ceci nous a rendus curieux : à quelle vitesse notre configuration essayait-elle les combinaisons ? Que se serait-il passé avec une méthode de chiffrement plus complexe comme l’AES-128 ?
Toutes nos archives protégées par un mot de passe sont-elles vraiment à 20 minutes du premier venu ?
| Combinaisons/seconde, attaque par force brute | Advanced Archive Password Recovery | Visual Zip Password Recovery Processor |
|---|---|---|
| Compression: aucune Cryptage : Zip 2.0 | 28 357 311 | 20 943 157 |
| Compression: aucune Cryptage : AES-128 | 9715 | échec |
| Compression: aucune Cryptage : AES-256 | 9713 | échec |
| Compression: Zip Cryptage : Zip 2.0 | 28 492 733 | 20 888 938 |
| Compression: Zip Cryptage : AES-128 | 9733 | échec |
| Compression: Zip Cryptage : AES-256 | 9760 | échec |
| Compression: RAR Stocker Cryptage : AES-128 | 213 | – |
| Compression: RAR Stocker Cryptage : AES-128, noms des fichiers | 202 | – |
| Compression: RAR Normal Cryptage : AES-128 | 213 | – |
| Compression: RAR Normal Cryptage : AES-128, noms des fichiers | 202 | – |
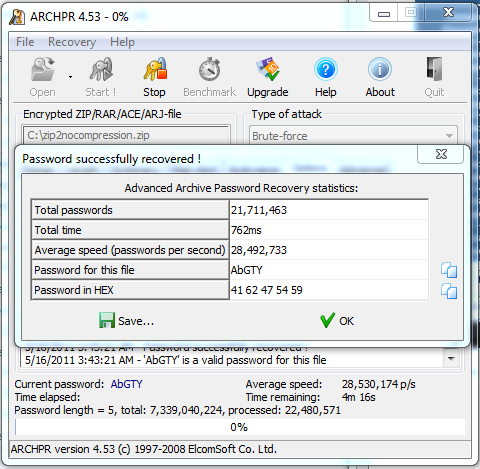
Comme on peut le voir ci-dessus, la compression n’a qu’un effet relativement mineur sur le nombre de combinaisons par seconde. En revanche le chiffrement en Zip 2.0 accuse le poids des ans par une faiblesse majeure : concrètement, un Core i5-2500K peut retrouver un mot de passe à cinq caractères en quelques instants vu qu’il peut tenter environ 28 millions de combinaisons par seconde. Advanced Archive Password Recovery comme Visual Zip permettent tous deux de trouver un mot de passe avec un cryptage Zip 2.0, mais le second devient inefficace avec l’AES-128 (problème logiciel).
Plus que la capacité du processeur à tester les combinaisons, c’est surtout la résistance des mots de passe qui nous intéresse ici :
| Durée de la recherche à 28 millions de combinaisons/seconde | Mot de passe entre 1 et 4 caractères | Mot de passe entre 1 et 6 caractères | Mot de passe entre 1 et 8 caractères | Mot de passe entre 1 et 12 caractères |
|---|---|---|---|---|
| Minuscules | instantanée | 11 secondes | 2 heures | 112 ans |
| Minuscules et majuscules | instantanée | 12 minutes | 22 jours | 451 345 ans |
| Tous caractères ASCII | 3 secondes | 7 heures | 8 ans | 701 193 345 ans |
Quand bien même on est en mesure d’essayer 28 millions de combinaisons par seconde, on voit que la probabilité de trouver la bonne finit par devenir infime lorsque l’on a un mot de passe long et complexe. La rupture se fait avec huit caractères : passe encore les 22 jours de calculs si les données sont vraiment importantes, mais si le mot de passe n’est pas uniquement composé de lettres majuscules et minuscules, il faut alors 8 ans de recherche.
Heureusement, Advanced Archive Password Recovery permet de mettre la recherche en pause et de la sauvegarder pour la prendre plus tard. Pour peu que l’on ait plusieurs machines à disposition, on peut vraiment gagner du temps en distribuant la charge de travail.
Cracker un mot de passe en GPGPU
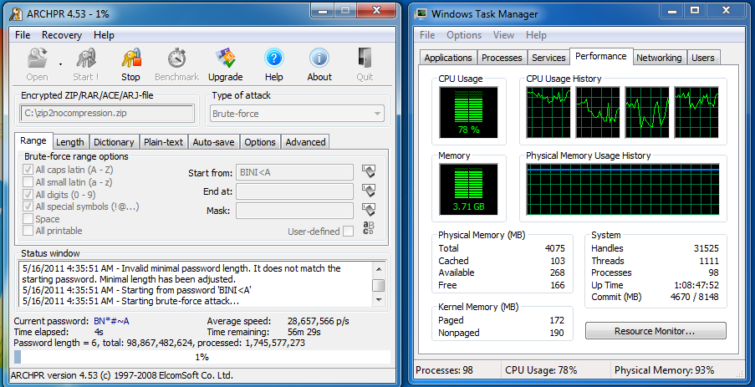
Comme on l’a vu, le principe d’une attaque par force brute est d’essayer un maximum de combinaisons aussi rapidement que possible, mais les processeurs modernes ne sont pas particulièrement bien optimisés pour ce faire. Notre configuration de test a beau pouvoir traiter 28 millions de combinaisons à la seconde, on constate également que tous les cycles CPU ne sont pas employés (rappelons que l’on est sur un processus essai/erreur répétitif). La capture d’écran ci-dessus montre que la fréquence est utile, mais surtout que le programme tire parti du parallélisme et pourrait donc afficher des performances supérieures avec plus de cores.
En matière de parallélisme, on sait qu’un processeur est généralement efficace mais que les ALU d’une carte graphique le sont souvent encore plus. AMD et NVIDIA avaient ainsi convaincu les acteurs du transcodage vidéo jusqu’à ce qu’Intel implémente Quick Sync dans Sandy Bridge avec le succès que l’on sait. Reste que l’on tient ici un domaine dans lequel le potentiel de calcul général des cartes graphiques actuelles devrait pouvoir être exploité.
Le crack des mots de passe en GPGPU a longtemps été la chasse gardée de la communauté académique, sachant que les acteurs travaillaient sur un code personnalisé qui n’a jamais débouché sur un programme commercial. Il existe aujourd’hui deux utilitaires GPGPU accessibles au grand public : Parallel Password Recovery et Accent Password Recovery.
Le premier est exclusivement optimisé pour CUDA. Ceci ne veut pas dire que la technologie GPGPU de NVIDIA est meilleure que l’AMD Stream, mais il faut tout de même souligner l’implication de la firme au caméléon dans ce domaine : NVIDIA s’est investi bien plus tôt qu’AMD et offre aux développeurs une pléthore de libraires de bas niveau nécessaires pour maitriser la technologie. La réponse d’AMD a été bien plus lente et à vrai dire, on constate encore des ratés avec l’accélération Stream lorsqu’elle est activée sur quelques programmes de transcodage bien connus. Ceci explique en partie pourquoi le second logiciel (Accent Password Recovery) semble lui aussi privilégier l’architecture NVIDIA. CUDA et Stream sont tous deux pris en charge, mais seules les cartes de la firme au caméléon sont optimisées pour attaquer le chiffrement Zip 2.0.
| GTX 460 | ||
|---|---|---|
| Attaque par force brute (combinaisons/seconde) | Parallel Password Recovery | Accent Password Recovery |
| Compression: Zip Cryptage : Zip 2.0 | 24 111 280 | 516 096 000 |
| Compression: Zip Cryptage : AES-128 | 185 072 | 166 800 |
| Compression: Zip Cryptage : AES-256 | 185 177 | 156 138 |
| Compression: RAR Normal Cryptage : AES-128 | 3493 | 4231 |
Le moins que l’on puisse dire c’est que l’optimisation est bien présente avec le cryptage Zip 2.0 ! Une GTX 460 permet donc de dépasser les 500 millions de combinaisons à la seconde, c’est-à-dire environ 18 fois plus qu’un Core i5-2500K. Concrètement, on est alors en mesure de retrouver un mot de passe à sept signes parmi tous les caractères ASCII en moins de 48 heures. Pour huit signes, on mettrait environ 168 jours.
| GTX 460 | ||
|---|---|---|
| Attaque par force brute Tous caractères ASCII Durée de la recherche | Mot de passe entre 1 et 6 caractères | Mot de passe entre 1 et 8 caractères |
| A 180 000 combinaisons/seconde | 50 jours et 20 heures | 1284 ans et 79 jours |
| A 24 millions de combinaisons/seconde | 9 heures et 9 minutes | 9 ans et 230 jours |
| A 500 millions de combinaisons/seconde | 26 minutes et 21 secondes | 168 jours et 17 heures |
Bien entendu le cryptage Zip 2.0 est plutôt dépassé et si WinZip continue de le proposer, c’est au nom de la compatibilité. L’AES (Advanced Encryption Standard) est maintenant l’algorithme de référence : il est inviolé à ce jour et bien plus difficile à paralléliser que le Zip 2.0, même si les éditeurs de logiciels s’y emploient sûrement.
Les performances s’effondrent littéralement lorsque l’on essaie de retrouver un mot de passe chiffré en AES, au point que le curseur de la souris partait en syncope sur notre configuration de test. Les attaques par force brute (seule solution à ce jour) sont extrêmement lentes : il faudrait plus de 13 ans pour retrouver un mot de passe à sept signes sur la base des 128 caractères ASCII.
| 2 x GeForce GTX 570 en SLI | ||
|---|---|---|
| Attaque par force brute (combinaisons/seconde) | Parallel Password Recovery | Accent Password Recovery |
| Compression: Zip Cryptage : Zip 2.0 | 45 412 290 | 1 492 279 088 |
| Compression: Zip Cryptage : AES-128 | 495 133 | 513 936 |
| Compression: Zip Cryptage : AES-256 | 496 244 | 513 880 |
| Compression: RAR Normal Cryptage : AES-128 | 13 904 | 14 605 |
Le GPGPU reposant intégralement sur le parallélisme, on devrait donc avoir de meilleurs résultats avec les 960 (2x 480) CUDA cores d’un SLI de GTX 570 plutôt que les 336 d’une seule GTX 460.
Une fois en place, les deux cartes font passer le chiffrement Zip 2.0 pour de la pâte à modeler. Grâce au code optimisé, on grimpe à 1,5 milliard de combinaisons par seconde : dans les faits, le temps nécessaire à retrouver un mot de passe à huit signes sur l’ensemble des caractères ASCII est réduit à deux mois environ.
En parallèle, le chiffrement AES reste solide puisqu’il faudrait presque 5 ans à raison de 500 000 combinaisons à la seconde pour venir à bout d’un mot de passe au-delà de sept signes.
Performances en attaque par force brute : NVIDIA vs AMD
Cet exercice repose intégralement sur l’échelonnement des performances. Il faut un maximum de cores à haute fréquence: deux GTX 570 n’ont que 2,8 fois plus de CUDA cores qu’une seule GTX 460 et pourtant, les performances sont triplées. Ceci s’explique du fait que les CUDA cores des GTX 570 affichent une fréquence supérieure (8 %).
De même, une GTX 590 affiche des résultats similaires à celui du SLI : la carte bi-GPU a certes plus de cores, mais ils sont aussi cadencés à une fréquence moins élevée. Toutefois, si le but est d’avoir des performances maximales, une paire de GTX 590 restera la configuration ultime chez NVIDIA.
En comparaison, les 3072 Stream processors de la HD 6990 fonctionnent à 830 MHz. Rappelons cependant que les Sp d’AMD ne sont pas directement comparables aux CUDA cores de NVIDIA.
Nous n’avons pu que brièvement essayer une paire de HD 5850 en CrossFire, ce qui n’a pas empêché d’arriver à des résultats impressionnants : les 2880 Sp permettent d’atteindre environ 1,1 million de combinaisons par seconde sur une archive chiffrée en AES-128. La solution ultime serait bien entendu de combiner deux HD 6990 mais même dans ce cas de figure, on dépasserait tout juste les 3 millions de combinaisons par seconde. Concrètement, il serait encore impossible de casser un mot de passe à huit caractères en moins d’un an.
| CUDA/Stream cores | Fréquence shader | |
|---|---|---|
| GeForce GTX 460 1 Go | 336 | 1350 MHz |
| GeForce GTX 570 | 480 | 1464 MHz |
| GeForce GTX 590 | 1024 | 1214 MHz |
| Radeon HD 5850 | 1440 | 725 MHz |
| Radeon HD 5970 | 1600 | 725 MHz |
| Radeon HD 6990 | 3072 | 830 MHz |
Il ne faut donc pas espérer en finir rapidement avec les mots de passe qui excèdent sept caractères, mais le fait est que nous regardons les pires cas de figure : c’est un peu comme si l’on recherchait une combinaison entre 00 et 99 pour constater au final que la bonne est 99. Dans la pratique ce n’est généralement pas le cas et le temps de calcul s’en trouve donc réduit.
Les programmes dédiés à la récupération des mots de passe comme ceux-là n’effectuent pas de recherche intégralement séquentielle, ce qui n’en fait donc pas une bonne solution pour la sécurisation des mots de passe. En toute vraisemblance, la récupération du mot de passe se produira à peu près à mi-parcours de la procédure, mais ceci ne change pas vraiment notre conclusion vu les laps de temps dont il est question. Le Zip 2.0 nous semble incapable d’offrir un niveau de sécurisation suffisant : s’il est clair que la récupération d’un mot de passe de neuf ou 10 caractères serait autrement plus longue que les exemples ci-dessous, ce serait tout à fait faisable avec quelques configurations comme celle utilisée pour le test.
| 2 x GeForce GTX 570 en SLI | ||
|---|---|---|
| Attaque par force brute Tous caractères ASCII Durée de la recherche | Mot de passe entre 1 et 6 caractères | Mot de passe entre 1 et 8 caractères |
| A 500 000 combinaisons/seconde | 18 jours et 7 heures | 462 ans et 116 jours |
| A 45 millions de combinaisons par seconde | 4 heures et 52 minutes | 5 ans et 49 jours |
| A 1,5 milliard de combinaisons par seconde | 8 minutes | 56 jours et 5 heures |
Sécurité : WinZip et WinRAR
Les mots de passe ne débloquent pas directement les fichiers chiffrés : il faut générer une clé de déchiffrement à partir du mot de passe et c’est exactement ce que nous avons fait jusqu’ici. Il y a là un goulet d’étranglement pour les attaques par la force brute : vu que la dérivation de clé représente 99 % du processus de récupération, il faut donc des ressources conséquentes pour en venir à bout.
WinZip et WinRAR utilisent tous deux la fonction de hachage cryptographique SHA-1 (Secure Hash Algorithm) pour dériver des clés, mais le mécanisme est différent. WinZip s’appuie sur la fonction PBKDF2 (Password-Based Key Derivation Function 2.0) et emploie l’algorithme SHA-1 à 2002 reprises pour générer une clé. Toutefois celle valeur est constante quelle que soit la longueur du mot de passe (64 caractères maximum), d’où le fait qu’un mot de passe de 10 caractères soit aussi facile à casser avec l’AES-256 qu’avec l’AES-128.
En comparaison, WinRAR utilise son propre système de dérivation de clé. Celui-ci nécessite (longueur du mot de passe x 2 + 11) x 4096 transformations en SHA-1, d’où le fait que les attaques par la force brute sont nettement plus chronophages sur des archives WinRAR.
| 2 x GeForce GTX 570 en SLI | ||
|---|---|---|
| Attaque par force brute (combinaisons/seconde) | Parallel Password Recovery | Accent Password Recovery |
| Compression: Zip Cryptage : AES-128 | 495 133 | 513 936 |
| Compression: Zip Cryptage : AES-256 | 496 244 | 513 880 |
| Compression: RAR Normal Cryptage : AES-128 | 13 904 | 14 605 |
Dans la pratique, on a tout de même autrement plus de chances d’oublier un mot de passe plutôt que de voir une de ses archives protégées tomber dans les mains de quelqu’un ayant beaucoup de temps et de moyens. Quand bien même cette personne aurait une configuration à la pointe, il lui faudrait plus de mille ans pour casser un mot de passe à 9 caractères pour une archive WinZip chiffrée en AES-128. Il est toutefois nettement plus facile de récupérer un mot de passe oublié si l’on sait à quoi il ressemble.
Imaginons par exemple un mot de passe à 10 caractères ASCII dont on connait les caractéristiques suivantes :
- Commence par e
- Finit par a
- Sans majuscules
- Un point d’exclamation
- Ne contient aucune des lettres suivantes : B, C, D, Q, T, U, V, W, X, Y, Z
On passe alors de 205 trillions à 1 trillion de combinaisons à essayer, ce qui est réalisable avec une paire de GTX 570. La récupération d’un mot de passe est par contre quasi-impossible avec WinRAR, à moins que celui-ci ne soit très court.
Conclusion
Nous avons été assez surpris après avoir essayé de récupérer le mot de passe d’une vielle archive WinZip. Le fait est que nous sommes à une époque où les donnes censées être protégées ne le sont pas autant qu’on le voudrait (le PSN en est un très bon exemple), ce qui est assez inquiétant quand on constate l’évolution de nos processeurs/cartes graphiques et l’utilisation qui peut en être faite.
Il y a encore une dizaine d’années, il était inconcevable de casser un mot de passe ASCII de 10 caractères dans un délai acceptable à moins d’utiliser une machine conçue pour cela. C’est précisément ce que l’EFF (Electronic Frontier Foundation) a réalisé en 1998 avec son Deep Crack : moyennant 250 000 $, un groupe d’experts a pu construire une machine mettant 1856 puces ASIC AWT-4500 en commun pour arriver à 90 milliards de combinaisons par seconde.
Treize ans plus tard, nous n’arrivons pas au même niveau avec notre configuration de test, mais il faut tout de même noter que notre SLI de GTX 570 affiche 1,5 milliard de combinaisons par seconde avec le cryptage Zip 2.0 : il s’agit d’1/60ème des performances de Deep Crack, pour moins d’un 1/100ème de son prix. Ceci revient à comparer des pommes à des poires vu que le chiffrement Zip 2.0 est dépassé, mais l’essentiel n’est pas là : les architectures graphiques massivement parallèles continueront de progresser à des prix accessibles, jusqu’au jour où sortiront des composants grand public capables d’atteindre les 90 milliards de combinaisons à la seconde.
En parallèle, nous avons vu qu’il valait mieux prendre ses distances avec le cryptage Zip 2.0 : il n’est maintenu que par souci de compatibilité et WinZip conseille l’AES pour une meilleure protection contre les attaques par la force brute.
Les attaques ciblées posent d’autres problèmes : à partir du moment où l’on utilise un mot commun dans un mot de passe, il devient vulnérable aux attaques par dictionnaire quel que soit le chiffrement utilisé. Un dictionnaire de Français courant compte environ 60 000 entrées, une encyclopédie 200 000, tandis qu’une simple GTX 460 peut gérer au moins 150 000 combinaisons par seconde contre un chiffrement AES. Quand bien même on ajouterait quelques variations, il ne faudrait pas plus d’une journée pour cracker le mot de passe :d’un point de vue fonctionnel, un mot entier revient à la même chose qu’une seule lettre.
Voici quelques écueils à éviter pour renforcer la sécurité de ses archives :
- Eviter les mots du dictionnaire : Le Petit Robert 2011 compte par exemple 60 000 mots, ce n’est rien pour une GTX 460.
- Eviter d’ajouter un chiffre en suffixe : ce n’est pas parce que l’on rajoute « 1 » à la fin d’un mot de passe qu’il devient plus sûr, vu qu’une demi-journée suffit à tenter tous les mots du dictionnaire et le chiffre manquant avec un SLI de GTX 570.
- Eviter les répétitions de mots ou lettres de substitution : Motdepassemotdepasse ne fait que doubler le nombre de mots à tester, ce qui n’est pas un obstacle vu la vitesse à laquelle les combinaisons sont tentées. M07d3p@553 n’est pas non plus un bon mot de passe vu que les crackeurs connaissent ce genre de transcription.
- Eviter les séquences courantes du clavier : Il n’est pas compliqué de rajouter AZERTY au dictionnaire de mot de passe à tester, mieux vaut donc éviter ce genre de raccourcis.
- Eviter les séquences numériques courantes : 314159 est un nombre facile à retenir vu qu’il s’agit de Pi ; il est aussi souvent testé.
- Eviter les données personnelles : numéro de sécurité sociale, numéro de téléphone, immatriculation, anniversaire etc. Nous sommes dans une époque où beaucoup d’informations personnelles sont en fait disponibles dans le domaine public, a fortiori quand on possède un compte Facebook/Twitter et consorts.
Le cryptage est aussi valable que le mot de passe qui le protège, or c’est justement la faiblesse des mots de passe symétriques (les clés de chiffrement et déchiffrement sont alors identiques). Le PGP (Pretty Good Privacy) et le chiffrement par certificat offrent des niveaux de protections extrêmement élevés, mais il est délicat de les utiliser au quotidien à moins de passer aux archives PKZIP. En premier lieu, il faut donc choisir un mot de passe à la fois long et complexe.
Fort heureusement, les mathématiques sont là pour nous aider : sur la base des caractères ASCII, la résistance d’un mot de passe sera 94 (taille du mot de passe) vu que chaque caractère supplémentaire rend le mot de passe 94 fois plus sûr. Quelques caractères en plus suffisent donc à rendre un mot de passe virtuellement inviolable vis-à-vis des attaques par la force brute : si les 7 298 831 534 994 528 combinaisons possibles avec un mot de passe à neuf caractères ne suffisent pas à être rassuré, on peut passer à 10 caractères pour atteindre les 699 823 827 359 474 784 possibilités.
Vu les résultats que nous avons obtenus pour cet article, une paire de HD 6990 devrait permettre de légèrement dépasser les 3 millions de combinaisons par seconde contre un cryptage AES. Concrètement, il faudrait alors 7397 années avec l’AMD Stream activé pour rechercher toutes les combinaisons possibles avec un mot de passe de 10 caractères.
Peut-être qu’il sera possible à l’utilisateur moyen d’accéder à des possibilités de calcul parallèle suffisantes pour ce genre de tâche à l’avenir. Le calcul distribué constitue la prochaine étape, sachant que Parallel Pasword Recovery travaille déjà sur la répartition du calcul par accélération GPU.
Il n’y a pas de quoi se faire du mauvais sang pour le moment, mais il est important d’être conscient du niveau de sécurité de ses archives. C’est justement le rôle des logiciels pour la récupération des mots de passe, vision d’ailleurs partagée par WinZip. Tom Vaughan (son vice-président) a ainsi déclaré : « Pour moi, les programmeurs de logiciels pour la récupération de mots de passe sont des white hats et non pas des black hats. Ce sont les logiciels que l’on ne connait pas encore qui devraient nous inquiéter (développé par des black hats et plus rapides/capables de casser des sécurités que ce à quoi on s’attendait) ».
D’autre part, il ne faudrait pas perdre de vue que l’on ne peut pas acheter le/les logiciel(s) de référence : le cryptage personnalisé avance toujours plus vite que les solutions accessibles au grand public. Après avoir abordé ce qu’il vaut mieux éviter, voici quelques conseils pour le choix du mot de passe :
- Au moins neuf caractères
- Au moins une majuscule
- Au moins une minuscule
- Au moins un caractère spécial comme @ ou !
- Au moins un chiffre
.