Introduction
Après le raytracing il y a quelques semaines, nous poursuivons notre tour d’horizon des techniques de rendu qui pourraient, dans un futur proche, remplacer ou tout du moins compléter la rastérisation de triangles telle que nous la connaissons aujourd’hui. Comme vous avez pu le constater dans notre précédent article nous ne sommes pas particulièrement convaincus de l’intérêt du raytracing temps réel. Cette opinion se retrouve par ailleurs chez la plupart des développeurs de jeux vidéo et notamment une des célébrités du milieu : John Carmack. Celui-ci déclarait l’an dernier à nos confrères de PC Perspective :
« Mon opinion concernant le raytracing au sens classique du terme, consistant à calculer de façon analytique l’intersection de rayons avec une géométrie définie de façon conventionnelle, que ça soit des maillages de triangles ou des primitives de plus haut niveau, est que je ne suis pas convaincu que cette technique, qui est essentiellement ce qu’Intel met en avant, s’imposera comme la méthode de choix pour les taches de rendu principales. Il y a de nombreux avantages en faveur de la rastérisation d’un point de vue des performances, et de nombreux éléments qu’ils avancent concernant l’utilisation de techniques de culling efficaces pour éviter de référencer une grosse partie de la géométrie ne sont que des arguments fantômes car il est tout à fait possible d’obtenir des résultats similaires en utilisant les requêtes d’occlusion et le rendu conditionnel avec la rastérisation. Au final la rastérisation est simplement une utilisation largement plus efficace de la quantité de transistors que vous avez à votre disposition. »
Si John Carmack ne semble pas vraiment emballé par le raytracing ce n’est pas pour autant qu’il est particulièrement conservateur et souhaite voir la rastérisation de triangles perdurer comme technique de rendu inamovible. Comme nous vous le disions il y a un an, John Carmack a sa propre idée du futur du rendu temps réel et celui-ci implique le raycasting de voxels. Depuis l’an dernier Jon Olick a fait sa présentation au Siggraph et de nombreux détails ont été révélés, il est donc temps de s’intéresser de plus près à ce que nous réserve id Software.
Un peu d’histoire…
Les expérimentations de Carmack avec les voxels ne datent pas de l’an dernier, en fait tout ça date d’une dizaine d’années. Entre les moteurs de Quake/Quake II et celui de Quake III, John Carmack a réalisé plusieurs expérimentations avec de nouvelles techniques de rendu. Il a désigné l’ensemble de ses recherches sous le nom de code Trinity que beaucoup de joueurs ont vu comme un futur produit, la nouvelle génération de moteurs 3D de chez id Software alors qu’au final le moteur de Quake III est resté assez conventionnel comme il l’a révélé lui-même dans un de ses .plan datant de 1998 :
«Voici quelques notes sur les technologies que j’ai explorées durant la mise au point du moteur de Quake III/Trinity. J’ai consacré initialement plusieurs mois à des recherches assez ouvertes mais il s’est avéré finalement qu’aucune de ses recherches préliminaires n’ont eu de rapport avec les directions que j’ai finies par choisir. Ah tant pis, j’ai beaucoup appris au passage et cela paiera probablement dans quelques temps. »
Parmi ses expérimentations se trouvaient l’affichage d’octree de voxels. Voici ce qu’il déclarait peu de temps après la sortie de Quake III :
« J’ai écrit ces deux moteurs de rendu voxel au début du développement de Quake III et j’en suis arrivé au point où je pensais pouvoir pratiquement les faire tourner de façon logicielle mais ça aurait été à une résolution assez faible et comparé à ce que l’on pouvait faire à cette vitesse avec des triangles accélérés par le matériel, ça n’était pas rentable.
J’ai fait une analyse de ce que seraient les motifs d’accès mémoires, etc, on peut faire un raytracer de voxels en hardware avec nettement moins de matériel que ce que nous utilisons à l’heure actuelle pour les rasterizers de triangles et je pense que ça pourrait être une représentation visuelle beaucoup plus attirante dans de nombreux cas. »
Cette citation est extraite d’une interview de Firing Squad datant du début de l’an 2000, il y a prés de dix ans, on peut donc dire que cette idée trotte dans la tête de John Carmack depuis un bon moment.
Il est impossible de parler de voxels sans mentionner Outcast. Ce jeu sorti il y a plus de 10 ans (juillet 1999, voilà qui ne nous rajeunit pas) a marqué toute une génération de joueurs par ses multiples qualités mais aussi pour son moteur 3D si particulier à cette époque où les cartes 3D s’étaient imposées dans les PC des joueurs. En effet Outcast reposait sur un moteur de rendu totalement logiciel ce qui le rendait particulièrement gourmand, pour pouvoir faire tourner le jeu dans sa résolution maximale (un impressionnant 512×384 !) il fallait un processeur dernier cri (mais pas de carte d’accélération 3D). Mais la gourmandise n’est pas la seule raison qui fait que ce moteur 3D a marqué les esprits, son utilisation des voxels a également assuré au jeu un rendu véritablement unique.
Pour autant il faut relativiser quelque peu cette affirmation : si le jeu est resté (en compagnie des jeux de Novalogic) le porte étendard du rendu à base de voxels, en réalité il n’en utilisait qu’une forme assez simplifiée et uniquement pour le terrain. Tous les objets ainsi que les personnages étaient pour leur part des modèles polygonaux tout ce qu’il y a de plus classiques. Le terrain pour sa part reposait sur une heightmap (carte de hauteur), de ce fait il n’y avait qu’une seule hauteur possible pour chaque point du terrain, ce qui interdisait des structures complexes comme des arches par exemple.
Ce problème n’était pas vraiment rédhibitoire car ce type de structures reste assez rare dans la nature du fait des contraintes de la physique. L’affichage du terrain était assez simple et se faisait colonne par colonne. Pour chaque colonne une valeur maximale en Y était stockée (Y-Buffer) ensuite les pixels de la colonne en question étaient remplis du bas de l’écran vers le haut uniquement si leur valeur Y était supérieure à celle stockée dans le Y-Buffer. Cette méthode de rendu permettait une suppression très efficace et très simple des parties non visibles de la scène.
Après ce retour dans le passé il est temps de voir maintenant ce que nous réservent les voxels dans le futur.
Un peu de technique (voxel)…
Avant d’entrer dans les détails de l’algorithme il faut que nous précisions certains termes : voxels, octree, raycasting… tout ça c’est bien joli mais tout le monde n’a pas un dictionnaire Carmack/Français à sa disposition.
Tout comme pixel est la fusion de deux mots : picture element, signifiant donc élément d’une image, un voxel est la fusion des mots volume et pixel, c’est donc un élément de base d’un volume. Pour imaginer ça de façon plus simple, repensez donc aux blocs de lego de votre enfance, vous pouviez construire à peu près tout et n’importe quoi avec quelques petits cubes de base. Les voxels partent du même principe : un volume est approximé par un assemblage de blocs cubiques. On a donc une représentation volumique alors que les maillages de triangles ne représentent en quelque sorte qu’une coquille vide, une peau qui entoure le volume.
Si les voxels ont été utilisés à de nombreuses reprises dans les jeux vidéo, c’est surtout dans le domaine médical qu’ils sont traditionnellement employés. En effet cette primitive est particulièrement adaptée à la reconstruction de volumes à partir de successions d’images de coupes transversales que peuvent fournir un IRM notamment. Cependant la représentation de volumes à l’aide de voxels n’est pas exempte de défauts : le monde n’est pas constitué d’un assemblage de petits cubes, aussi il est impossible d’obtenir une représentation exacte de la plupart des volumes à l’aide de voxels. Ainsi l’image suivante montre un cas particulièrement défavorable avec une approximation grossière d’un tore à l’aide de voxels.
Il faut toutefois relativiser ce défaut dans le cadre des jeux vidéo : les maillages de triangles utilisés par nos jeux ne sont déjà qu’une approximation d’un volume et tout comme lorsqu’on affine une représentation en utilisant plus de triangles il est possible d’utiliser une grille plus fine de voxels pour limiter ce défaut, mais c’est alors que le principal inconvénient des voxels surgit : sa consommation mémoire.
Une simple grille de 1024 voxels dans chaque dimension occupe ainsi : 1024 x 1024 x 1024 * 4 (RGBA) = 4 Go de mémoire ! Et une telle résolution est loin d’être exagérée. Utiliser les voxels de cette façon est donc absolument inenvisageable. Heureusement il existe une solution pour limiter cet inconvénient : les octrees ou arbres octaux.
Un peu de technique (octree, raycasting)…
Un arbre en informatique est une structure de données fréquemment utilisée car elle permet d’agencer ces données de façon hiérarchique. Tout le monde l’utilise de façon quotidienne sans même s’en rendre compte en manipulant les fichiers de son ordinateur, en effet les systèmes de fichiers emploient une structure arborescente : il y a la racine du disque dur qui contient plusieurs fils (les dossiers), eux même contiennent d’autres fils (des sous dossiers) et ainsi de suite jusqu’aux feuilles (les fichiers). Cet exemple devrait vous donner une idée intuitive d’un des intérêts de l’utilisation d’arbres : accéder aux éléments d’un arbre équilibré est nettement plus rapide que si tous les éléments étaient éparpillés.
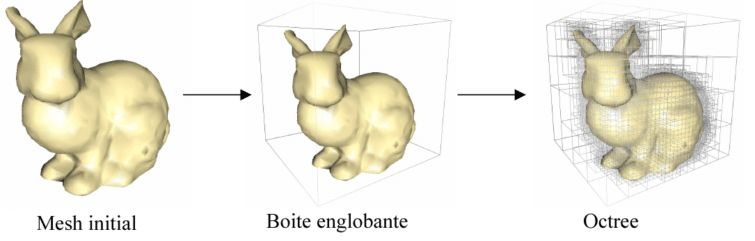
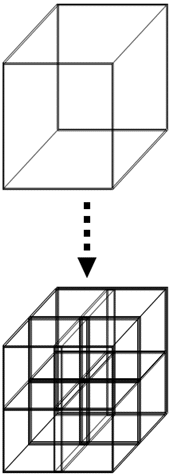
Les nœuds d’un arbre peuvent avoir un nombre différents de fils : lorsqu’il y a au plus deux fils on parle d’arbre binaire, zéro ou quatre fils arbre quaternaire et enfin lorsqu’il y a zéro ou huit fils on parle d’arbre octal. Mais quel est l’intérêt de ces arbres dans le cas qui nous intéresse ? Jusqu’à présent nous utilisions les voxels selon une grille régulière ce qui en fait gaspillait énormément de données pour encoder du vide, les octrees permettent d’utiliser plus efficacement l’espace mémoire en utilisant la résolution la plus fine uniquement là où c’est nécessaire. Penser en 3 dimensions n’est pas la chose la plus aisée qui soit et n’est pas facile à représenter dans un article, nous allons donc commencer par présenter ça de façon bidimensionnelle.
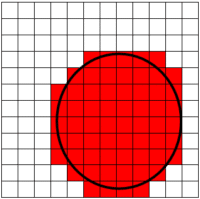
Voici l’approximation du cercle, avec une grille de résolution 12 x 12. L’approximation est grossière faute d’une résolution suffisante et cependant une grosse quantité de cellules sont blanches et donc inutiles. Si nous utilisions un quadtree voilà ce que nous obtiendrions :
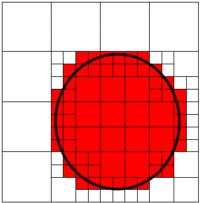
La construction du quatree est simple : on part de l’image initiale que l’on subdivise en deux selon les deux directions, nous obtenons quatre quadrants. Lorsqu’un quadrant est soit vide, soit entièrement plein l’algorithme s’arrête là. Si le quadrant n’est que partiellement rempli alors on subdivise de nouveau ce quadrant en quatre et ainsi de suite. L’algorithme s’arrête lorsque tous les quadrants sont homogènes c’est-à-dire uniformément vides ou pleins, ou plus traditionnellement lorsqu’une profondeur donné a été atteinte (dans l’exemple ci-dessus nous nous sommes arrêtés à une profondeur d’arbre de 4 c’est-à-dire une division de 16 dans chaque dimension). Comme vous pouvez le constater même avec notre exemple basique le résultat obtenu est un peu plus fidèle au cercle initial et pourtant nous utilisons moins de données (97 nœuds ou « cases » si vous préférez dans ce cas contre 122 avec la grille régulière). Un octree est une simple extension de cette technique à 3 dimensions.
En pratique le gain en espace mémoire à définition égale est un peu moins important qu’on pourrait le penser de prime abord, en effet dans le cas d’une grille régulière la position des voxels est implicite. A l’inverse dans le cas d’un octree chaque nœud doit conserver un « lien » vers chacun de ses fils. En pratique il faut donc pour chaque nœud conserver 8 pointeurs en plus de la couleur et de la normale du voxel.
Mais ce n’est qu’un petit inconvénient face aux nombreux autres avantages de l’octree, pour bien comprendre les apports les plus importants de l’octree il faut tout d’abord décrire la façon dont cette structure de donnée est affichée. Il existe plusieurs manières d’afficher des voxels mais la technique choisie par id Software est le raycasting, c’est celle-ci que nous allons décrire.
Raycasting
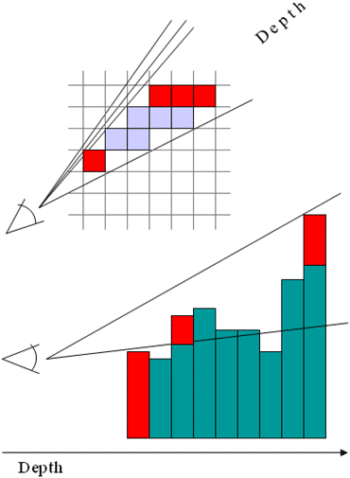
Tout comme le raytracing, le raycasting repose sur le lancer de rayons pour chacun des pixels de l’image, mais là où il diffère c’est que dès qu’une intersection a été trouvée l’algorithme s’arrête là et ne lance pas de rayons secondaires.
Par conséquent le raycasting est plus rapide que le raytracing car comme nous l’avons vu dans notre précédent article ce sont les rayons secondaires qui posent problèmes du fait de leurs accès mémoires. Autre avantage : calculer l’intersection de rayons avec les voxels est beaucoup plus rapide qu’avec des triangles. De plus il est inutile de construire une structure de données supplémentaires pour accélérer ces calculs d’intersection : l’octree est à la fois l’ensemble des données (géométrie et textures) et la structure d’accélération.
Les avantages du Sparse Voxel Octree
Intéressons nous maintenant aux avantages de notre octree de voxels dans le domaine du rendu. Le principal intérêt de cette structure de donnée est qu’elle permet de résoudre de façon élégante le problème de niveaux de détails des textures mais aussi de la géométrie le tout avec un seul algorithme ! En effet comme nous l’avons sous entendu dans le paragraphe précédent chaque nœud de l’octree contient une information de couleur, on peut par conséquent se débarrasser des textures 2D que nous connaissons, ou plus précisément, l’octree est à la fois la texture ainsi que la géométrie.
Par conséquent le problème de niveaux de détails (LoD) qui auparavant devait être géré pour la géométrie et pour les textures de façon totalement indépendantes se résume à un seul système désormais : gérer le niveau de détail de l’octree et il s’avère que cela peut se faire très simplement. Le principe est en quelque sorte une extension du mipmapping que l’on emploie pour les textures. L’objectif du mipmapping est d’essayer de conserver des texels (les éléments de la texture) d’une taille la plus proche possible d’un pixel. Pour cela plusieurs résolutions de la texture sont précalculées et stockées et le hardware adapte le choix du niveau de mipmap en fonction de la taille de la texture à l’écran.
Il est possible de faire quelque chose de similaire avec les octrees de voxel, le choix du niveau de détails se fait dynamiquement : dès que la taille d’un voxel est inférieure à la taille d’un pixel on arrête la traversée du rayon dans l’octree à ce niveau là. Il suffit donc dans chaque nœud de stocker la moyenne des informations contenues dans ses fils pour obtenir une gestion des niveaux de détails de manière très simple. Ce mécanisme est parfaitement adapté à un système de streaming, un peu à l’image de ce qu’emploie déjà id Software pour les MegaTexture : seules les portions de l’octree qui sont nécessaires sont stockées en mémoire vidéo, une autre partie réside en mémoire centrale pour accélérer les accès suivants mais surtout la grosse majorité de l’octree reste tout simplement sur le support de stockage.
La conséquence est qu’on dispose en effet d’une quantité de géométrie (et de textures comme nous l’avons vu) quasiment illimitée : l’octree peut être aussi détaillé qu’on veut, à l’exécution la quantité de mémoire et le temps d’affichage resteront (relativement) constants. La seule limite ici concerne donc le temps que les artistes pourront consacrer à la création de cet octree et les limites physiques des supports de stockage des machines de prochaine génération.
Soyons clairs : il est possible de résoudre ce problème de différentes manières, les systèmes de textures virtuelles (MegaTexture ou Sparse Virtual Textures) ont déjà résolu le problème pour les textures et seront intégrées aux principaux moteurs 3D l’an prochain (CryEngine 3, idTech 5…). Le cas de la géométrie est plus compliqué à résoudre mais il existe plusieurs pistes pour résoudre ce problème. La solution la plus simple consiste à précalculer plusieurs versions d’un mesh à des résolutions différentes et de sélectionner la plus adaptée en fonction de la distance du mesh à la caméra. Cette solution basique est simple à mettre en œuvre mais les artefacts visuels qui surviennent en passant d’un niveau de détails à un autre sont importants.
Les avantages du Sparse Voxel Octree (suite)
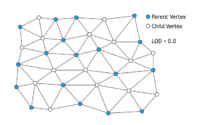
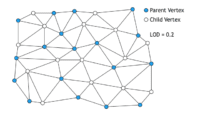
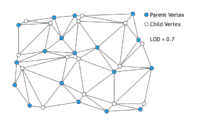
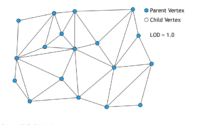
De nombreux chercheurs ont donc travaillé sur des manières de rendre continu le passage d’un niveau de détails à un autre, on parle de progressive mesh. L’idée consiste en fait pour chaque niveau de détails à séparer les sommets en deux groupes : les sommets parents, et les sommets enfants. Lorsque le niveau de détails diminue, les sommets enfants se rapprochent progressivement de leurs parents. Lorsque le niveau de détails atteint une nouvelle valeur entière les sommets enfants sont supprimés de même que toutes les arêtes qui les connectaient à leurs parents.
Cette technique fonctionne assurément mais elle n’est pas complètement automatique : elle demande aux artistes un travail supplémentaire pour indiquer quelles sont les arêtes importantes à conserver. Qui dit travail supplémentaire dit donc moins de temps disponibles pour peaufiner les modèles.
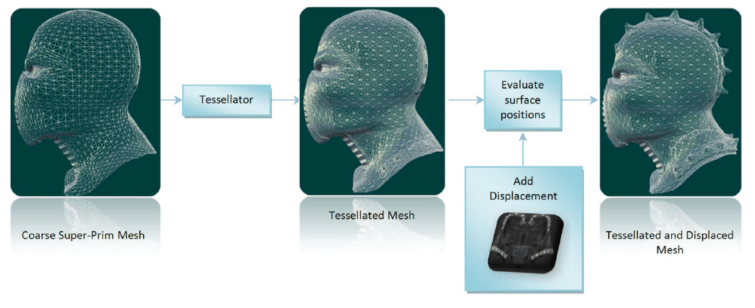
Une autre façon de résoudre le problème, dont on va beaucoup entendre parler prochainement avec l’arrivée des cartes DirectX 11 est la tesselation de primitives de plus haut degré (patchs) couplé éventuellement au displacement mapping. Cela fait des années qu’on nous promet l’arrivée de cette technique (Ahh la Parhelia…) sans que l’on voie de résultats concrets mais cette fois ce pourrait être la bonne.
Encore une fois cette technique est valable et risque d’avoir un certain succès vu les efforts de Microsoft et d’AMD pour pousser les développeurs dans cette direction, mais l’octree de voxels reste une alternative séduisante. Comme nous l’avons vu il permet de résoudre le problème de la géométrie et des textures avec un seul algorithme, de plus la sélection du niveau de détails est très facile : évaluer la taille d’un voxel à l’écran est simple, c’est plus compliqué pour un triangle.
Les limites
Cette technique a beau être séduisante elle n’en est pas pour autant dénuée de défauts. Le principal problème vient du fait que la construction de l’octree est coûteuse, par conséquent il n’est pas vraiment envisageable de modifier la structure de données à l’exécution. Cet inconvénient rend l’utilisation d’un octree de voxels pour la géométrie dynamique particulièrement compliquée. La proposition d’id Software pour contourner ce problème consiste à utiliser l’octree uniquement pour la géométrie statique, tous les éléments dynamiques de la scène seraient affichés en utilisant la bonne vielle rastérisation de triangles.
Il est dommage que le franchissement d’un cap visuel soit accompagné d’une telle restriction, en effet lors d’un changement de génération les joueurs s’attendent également à franchir un cap en matière d’interactions avec le décor. Lorsqu’on parle de voxels la première réflexion des joueurs consiste à penser à des mondes enfin destructibles, s’imaginant pouvoir tirer dans un mur et voir la géométrie s’altérer, révélant diverses couches de matériaux, mais pour le moment il semble que ça ne soit pas vraiment envisageable. Nous sommes bien partis pour conserver nos murs indestructibles quelques années encore.
Un autre problème concerne le système de streaming, comme nous l’avons vu cette technique de rendu est particulièrement adaptée pour augmenter le niveau de détails au fur et à mesure qu’on se rapproche progressivement d’un objet, le système se chargeant de ramener les données de l’octree en tâche de fond et du fait de la façon dont ses données sont organisées tout cela peut se faire de manière fluide. Mais que se passe-t-il lorsque nous nous téléportons à un autre endroit du monde ? Toute la géométrie est unique et le système de streaming est pris à défaut. Il faut donc s’attendre à voir une géométrie très basique pendant un moment, puis à la voir s’affiner au fur et à mesure, ou bien voir les game designers contourner ce défaut en évitant ce genre de situations. Ce problème n’est pas unique aux octrees de voxels, tous les systèmes de streaming reposent sur l’hypothèse d’une variation relativement continue du niveau de détails et sont pris à défaut dans le cas de changements brutaux, mais actuellement ça ne concerne que les textures et si voir une texture de basse résolution pendant une seconde ou deux est désagréable, voir un octree de basse résolution risque d’être visuellement assez affreux.
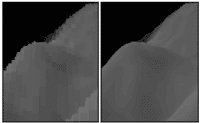
Un autre inconvénient que l’on peut recontrer avec les voxels concerne la pixellisation. En effet si l’on se contente d’afficher la couleur des voxels que le rayon intersecte, il est possible de discerner les limites des cubes ce qui donne un effet old-fashion très déplacé pour une technique qui se veut le futur des techniques de rendu. Heureusement il est possible de résoudre ce problème en utilisant le filtrage trilinéaire : au lieu de filtrer dans les deux dimensions comme avec les textures il faut cette fois filtrer selon les trois dimensions.
Enfin dernier challenge à relever, malgré l’avantage procuré par la structure d’octree, l’espace mémoire nécessaire pour stocker un monde entier sous forme de voxels reste énorme. Comme nous l’avons vu ça n’affecte pas vraiment les ressources nécessaires à l’exécution, mais en revanche pour pouvoir manipuler puis stocker et enfin distribuer de telles structures de données id Software va devoir travailler à de sérieuses techniques de compression. Jon Olick donne quelques indications à ce sujet et semble satisfait des taux de compression qu’il a obtenus.
Conclusion
Le rendu 3D temps réel vit une période particulièrement faste. Avec l’avènement des GPU de plus en plus programmables de nombreuses approches jusqu’ici inenvisageables ressurgissent pour tenter de résoudre les problèmes auxquels nous sommes confrontés. Le raycasting d’octree de voxels est une technique particulièrement prometteuse pour augmenter de façon drastique la complexité géométrique des jeux de demain. Evidemment tout ceci reste encore à l’état d’expérimentation, la démonstration de Jon Olick au Siggraph tient plus de la démonstration de faisabilité qu’autre chose et de nombreuses interrogations restent en suspens.
Une des questions qui se pose et qui sera déterminante pour l’avenir de cette technologie concerne les outils d’édition qui seront fournis aux graphistes. Jon Olick voit pour sa part une évolution du système actuellement utilisé pour les MegaTexture grâce auquel les artistes peuvent appliquer des tampons pour ajouter du détail à la texture. Un tel système au lieu de modifier la normal map viendrait modifier directement la géométrie dans le cas de cette technologie. Mais pour l’instant tout cela reste à l’état de concept et on le sait, faire de jolies démos est loin d’être la partie la plus difficile, il faut ensuite pouvoir transformer ça en un produit fini suffisamment stable et efficace.
Malgré tout il est particulièrement intéressant de voir un modèle de plusieurs millions de polygones (7 millions pour le modèle initial issu de ZBrush) à 60 images/seconde sur une carte de génération actuelle. Ces premiers résultats sont extrêmement prometteurs pour le matériel qui sera disponible à la sortie des jeux exploitant cette technique. Vu le temps de développement des jeux actuels et étant donné qu’id Software ne prévoit pas de sortir Rage avant l’année prochaine, il y a de grandes chances pour que nous devions encore attendre 3/4 ans pour voir ce type de rendus se démocratiser.
